Quantum paradoxes: Popping the bubble with Shor's algorithm.

The article was prompted by the first demonstration of a generic Shor’s algorithm implementation on scalable hardware. In addition, the release of the NSA advisory last year to avoid ECC codes in the interest of preventing quantum computer (QC) attacks against cryptography sent ripples through the security industry. Many questions were raised, like, “is it a cover-up?” and “are they using backdoors?” While such questions are best left to speculators, the threat that QCs have on existing cryptographic security is real and grows with each paper published on the latest QC implementations. A paradox unfolds when realising that quantum mechanics could, in turn, ensure secure transmission of information by utilising the fact that quantum states cannot be reliably copied, which leads to secure quantum key distribution.

This article delves into the mechanics of Shor’s algorithm on an algorithmic level, showing how a mathematical problem can be made solvable by a quantum computer. Furthermore, the implications of currently realised quantum computers and their impact on the security of cryptography are introduced. Follow-up posts will introduce the reader to the various QC designs and the implication that each design has on the problems that can be solved with each architecture. The possibilities that QCs will introduce are large, and understanding how to position oneself to maximally gain from as well as protect against this new technology is invaluable.

At the root of the QC paradox is the large computational gains that QCs are expected to unlock. Modern cryptographic implementations rely on trapdoor functions - functions that are straightforward to compute in one direction while being computationally intractable in the other direction. One such example is that used in the RSA algorithm. The core mathematical trapdoor function used in RSA relies on multiplying two very large prime numbers. As it turns out, it is tremendously difficult to reverse this operation to regain the original two prime numbers. Enter the QC and its massive computational power.

The key to finding the two primes in RSA, p and q where p x q = N, is to formalise an algorithm that can be performed to find the primes efficiently. The best-known implementation of this method is called Shor’s algorithm, named after its author Peter Shor who published the method in 1994. The first step is called modular exponentiation which attempts to use the RSA public key N in an equation until it finds an even repetition of values. For example, a particular choice of values gives an equation that repeats every four steps. If the equation is given by

and we choose a = 7 and N = 15 then,

This equation is solved by substituting positive integers for x, a plot of the equation is given below.

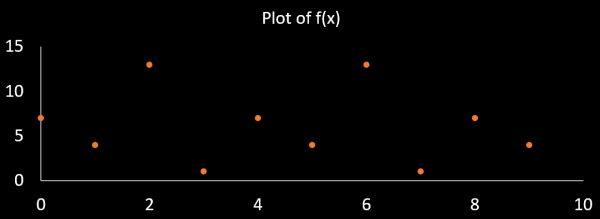
The repetition rate of this function is 4 (r = 4). Now we can find the greatest common divisor (GCD) of two numbers calculated as 

and

It can be noticed that 5 x 3 = 15 which is the value of N. Hence, we have discovered the prime numbers that make up 15.

The next challenge is to implement this algorithm in a QC to produce the result much faster. For this, we require an algorithm that will solve for the repetition rate of the modular exponentiation. A well-known algorithm for period finding is the Fourier transform. To the inexperienced, the Fourier transform can seem unintuitive, but there exists a classical analogue for the mathematics involved. Think of a piano with many strings, each connected to a key that, when struck, will produce a specific musical frequency. The Fourier transform does exactly the reverse of a piano, it takes an input signal, and tells you which combination of keys was pressed to produce that signal. All that is left to do then is to translate the key (or keys) that the Fourier transform indicates to their corresponding period of repetition (or frequency).

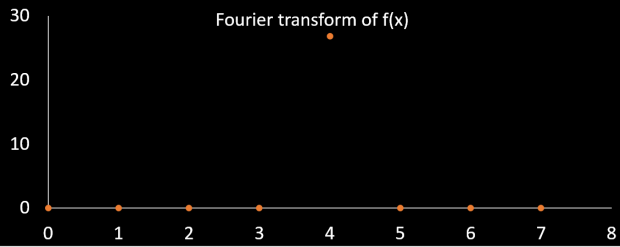
It can be seen that key zero and four are identified by the Fourier transform as being present in f(x). Key zero means that that part of the signal has zero repetition rate, key four, in this case, responds to a repetition rate of every four values of f(x) and key eight would correspond to a repetition for every two values of f(x). The values repeat beyond eight as a consequence of how the Fourier transform works, and we search for the answer in the key range 1-7. We see that the previously identified value of r = 4 is found by the Fourier transform, hence, we have a method of determining the repetition rate with an algorithm.

The QC implementation incorporates the modular exponentiation and Fourier transform in quantum mechanical hardware. Knowledge of the theory of quantum mechanics itself is required to fully understand how Shor’s algorithm is implemented. But in summary, the implementation of quantum gates seeks to evolve the quantum state of the QC in a controlled way such that the state after application of the quantum gates would be likely to correspond to the result of the mathematical algorithm implemented.

What is important for the discussion here, however, is being able to distinguish between the different quantum computers and what their implications are for the security of cryptography. The company D-Wave currently manufactures and sells a QC with 1000 qubits. What is the implication of this for the security of communications? A follow-up post will discuss this in more detail by describing the limitations that the D-Wave QCs have, what adiabatic quantum computation is, and why other architectures with much fewer qubits are more successful at solving certain problems. The short answer is that while many qubits are available in D-Wave processors, their limited programmability is unlikely to provide a means to program a usable quantum factoring algorithm at present.

The question remains whether present-day cryptography is under threat of compromise in the near future. To understand this threat, the discussion above on Shor’s algorithm and a further discussion on adiabatic quantum computation (D-Wave) is important. But regardless of architecture, the challenge of performing factorization on a very large RSA public key reduces to one problem – having enough programmable qubits to contain the entire factoring operation. An investigation by Proos and Zalka in 2004 found that a 1024 bit RSA key would require about 2000 qubits to run Shor’s algorithm. Manufacturing a QC that maintains programmability across that many qubits is a large engineering challenge. Simply put, the security of trapdoor function cryptography used currently is dependent on how hard it will be to construct QCs with enough qubits to break a given key length.

The difference in the number of qubits required to factor ECC and RSA puts the NSA’s statement shunning ECC cryptography into perspective. According to Proos and Zalka, the equivalent strength ECC key of 160 bits would require 1000 qubits to break. Compared to the 2000 qubits required to break a 1024 bit RSA key, it becomes evident that ECC and RSA key strengths are much different when quantum algorithms are involved, and it follows that large RSA keys would provide security against QCs further into the future than the significantly shorter but otherwise comparable ECC keys. In 2011, it was shown that adiabatic quantum computation with an optimisation algorithm, using four qubits, could solve the prime factors of the number 56153 (16 bits). Also, the implementation discussed by MIT News mentioned earlier required the use of 5 qubits, which is a large reduction in the number of qubits over the original implementation by Shor (12 qubits) and is also a better than that achieved with the optimisations considered by Proos and Zalka. We can conclude that while the most efficient factoring algorithms are still being developed, and similarly while the construction of a powerful QC has not yet been achieved, cryptography as we know it is unlikely to be secure for as long as we would like. Advances in factoring algorithms together with a steady increase in programmability and qubit counts in QCs is likely to progress slowly but steadily.

Lately investment in quantum technologies has escalated. In 2015, Intel announced a partnership with Delft University of Technology for $50 m in funding. The UK has pledged £270 m for investment in quantum technology in the UK. NASA and the US DoD continues to invest in development as well. The University of Sydney recently opened a Nanoscience hub that will also pursue the development of quantum technologies while the University of New South Wales extended their Centre for Quantum Computation and Communication Technology. Given this large increase in funding in the recent years, QCs are more likely than ever to revolutionise industries.